From June 6 to 11, I attended the International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2021, which was held online, as a fully virtual conference. ICASSP is a huge conference that presents lots of papers with various topics, and that specifically dedicates sections to Audio and Signal Processing works. In this blog post, I would like to showcase the paper entitled “Segmental DTW: A parallelizable Alternative to Dynamic Time Warping” that has been presented by its author Timothy J. Tsai, a researcher at Harvey Mudd College, Claremont, CA, USA.
This work is in a continuity of several previous works from the author that aim at exploring variants of the standard Dynamic Time Warping (DTW) to propose a variety of applications that cannot be answered with the initial DTW algorithm, such as an offline accompaniment generator from solo recordings for known pieces, or a piano score following video maker. Here, the author proposes a method for parallelizing the initial DTW to speed up the alignment process.
The algorithm
Segmental DTW is a variant of DTW. DTW aims at aligning pairs of sequences. The sequences are time series, that are mostly represented by feature sequences extracted from the audio signal. At first, DTW calculates distances, or costs, between each pair of features. Then, it computes the cumulative costs of each possible alignment with dynamic programming. Finally, it retrieves the optimal alignment in following the path given by the lowest cumulative cost.
The previously described algorithm presents two main limitations. At first, the time complexity of the algorithm is quadratic. It depends directly on the length of each time sequence. Additionally, the algorithm is based on dynamic programming, whose alignment is calculated incrementally from the first to the last frame. Thus, the algorithm is not parallelizable.
In the presented paper, the author aims at proposing a variant of DTW, Segmental DTW, that can quickly compute an alignment that closely matches the baseline DTW alignment. Instead of computing the alignment between two full sequences directly, the proposed algorithm breaks down the problem into subalignments between one full sequence and all non-overlapped segments extracted from the other sequence.
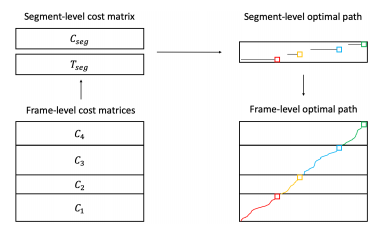
The algorithm is illustrated in Figure 1. The first step is described at the bottom left-hand corner. In this matrix, both time sequences are represented respectively along with the horizontal and vertical axis, the beginning being at the bottom left-hand corner. The vertical sequence is divided into segments of the same length. In the example, four segments are represented, from C1 to C4. For each segment, the algorithm applies Subsequence DTW that calculates the cumulative frame-level cost matrix between the segment and each possible subsequence in the vertical axis. The algorithm focuses only on subsequences that have a length in between half and double of the segment length. Musically speaking, this corresponds to tempo variations included between 0.5 and 2 times the reference tempo in the segment. At this point, the minimal value of all cumulative costs present in the last row of the cumulative cost matrix represents the best match between the segment and a subsequence ending at this index. Each cost matrix can be computed independently, i.e. in parallel.
As the second step, the algorithm creates the Cseg matrix in concatenating all lasts rows of previously calculated cost matrices. Cseg represents a segment-level cost matrix. It has the advantage of being smaller than the initial frame-level cost matrix.
The third step aims at connecting the segments between themselves and retrieving the global segment-level optimal path. This is done by applying dynamic programming with two allowable transitions. The first transition (0, 1) allows navigating between optimal subsequences in the horizontal axis for a given segment. Its weight is fixed to 0, which means that we do not accumulate costs in a segment, the goal is to select only one subsequence per segment. The second transition (1, N/(2K)) corresponds to the transition between a selected (the weight is set to 1) subsequence and the starting search point of the next segment. Because we search for subsequences that have a minimum distance of half of the segment length, we start the search from a length corresponding to N/(2K), where N/K is the length of the segment for an initial vertical sequence of length N and a fixed number of segments K. This strategy aims at finding the optimal path through Cseg. The path is composed of one element per row. The elements are in increasing order and at least separated by a minimal distance of N/(2K) in the vertical axis.
The fourth and last step retrieves the frame-level optimal path for the segment-level path. Each selected element in Cseg indicates the final index of the corresponding subsequence. This is done by backtracing each cumulative cost matrix from the selected element. This step is also computed in parallel.
The resulting path given by Segmental DTW can be discontinuous at segment borders. The author investigates the restriction to be strictly monotonic with the help of Tseg, the matrix shown at the top left-hand corner of Figure 1. In this matrix, each row corresponds to the starting indexes of all optimal subsequences in the horizontal sequence ending at the corresponding index. Thus, this is computed in backtracing each cumulative cost matrix of each segment from every possible ending location. This extension requires lots of additional computation and from experiments, the resulting optimal path is less accurate than the previous method. Thus, this method is no more detailed here.
Accuracy and speed
The following experiments are evaluated on the Chopin Mazurka dataset. It gathers pairs of audio recordings annotated at the beat level.
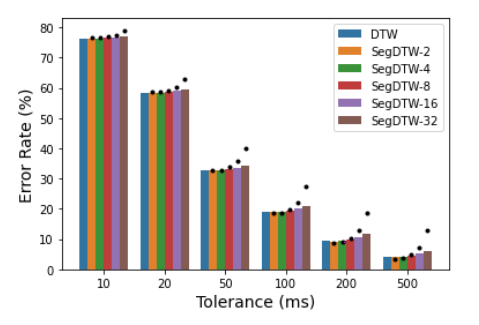
Segmental DTW and DTW do not give the same alignment path. This is due to the allowed discontinuities at segment boundaries. The more segments there are, the more different the paths are. In Figure 2, the author compares the error rate given by DTW and Segmental DTW with different numbers of segments (from 2 to 32). DTW can be seen as a special case of Segmental DTW where the number of segments is set to 1. For each error tolerance, the conclusions are identical: a small number of segments gives an error close to DTW whereas a large number of segments gives a larger error rate.
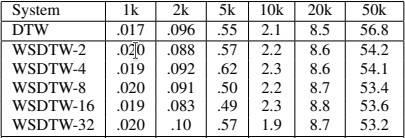
Segmental DTW adds additional steps to compute the alignment path. Even if steps 1 and 4 are parallelizable, an interesting question would be to know, if all the steps require more runtimes if they are computed on a single thread. Figure 3 shows that, for all cost matrices from size 1k (i.e. 1000x1000) to 50k (i.e. 50kx50k), DTW and SegmentalDTW require the same computation time. Thus, each parallelizable step is directly saving time.
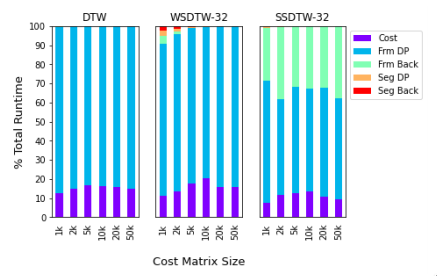
From the previous experiment, the next question is to know what is the percentage of runtime that can be parallelized. Figure 4 shows that, for cost matrices bigger than 5k and in using 32 segments, more than 99% of the runtime is parallelizable. This experiment shows that the proposed algorithm shorten drastically the alignment computation time.
Conclusion and insights
The author shows through his work a possible alternative to DTW that can parallelize almost all of its runtime without losing too much accuracy. The method is particularly interesting because it can also answer different problems that are well-known in the Music Information Retrieval community. Last year, the strategy to segment one of the sequences was already used to tackle audio-to-score alignments where repeats and jumps appear at unknown locations. Presented at ISMIR 2020 under the name Hierarchical DTW, the algorithm considers each score line as a segment, searches for the most probable subsequence in the audio recording for each score line, and finally connects the segments to output the optimal alignment path.
The idea of applying Subsequence DTW between an audio segment and a whole recording inspired my research in real-time Opera tracking. The task is challenging because the tracker has to be robust to deviations from the score, acting, or unknown skip and repeat sections that tend to interfere with the tracking process. Computing Subsequence DTW between segments received in real-time and the whole score permits the tracker to be sensitive to sudden score jumps or to redirect the tracker if it gets lost.
I will be looking forward to the next contributions of the author!