Here we take a look at a lovely paper by Fred Bruford et al. that presents and evaluates a set of engineered features for drum pattern analysis in the symbolic domain1.
It gathers both new and pre-existing features in literature, grouped in rhythm features, similarity metrics, and microtiming features. The final toolbox, written in Python, is evaluated on drum loop similarity perception experiments, where the authors are able to find significant correlations between feature values and similarity scores.
Toolbox
The Groove Toolbox is a comprehensive framework for modelling perceptual qualities of drum loops in the symbolic domain. It builds on previous research on drum loop analysis and, while not studying data-driven approaches yet, it provides a cohesive and interpretable set of perceptually motivated features.
The authors decided to implement those pre-existing algorithms that were proven to be perceptually relevant and that could handle different onset velocities. They also introduced four microtiming features and two similarity models. These similarity models are the fuzzy hamming distance, a variant of the hamming distance that accounts for minimal onset deviations, and a new structural similarity metric based on a transformation model2 that removes ghost notes and ornamentations to facilitate modelling.
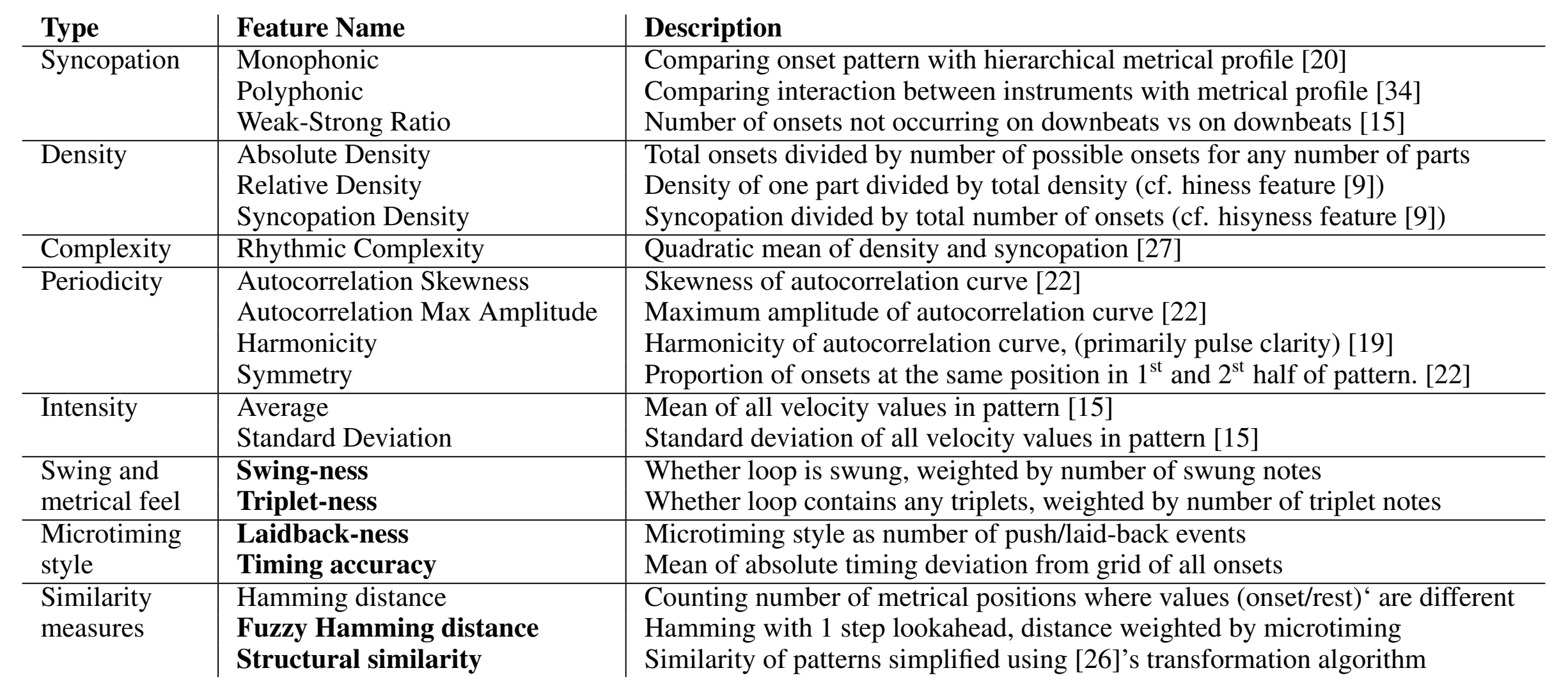
List of features and similarity measures currently implemented in the GrooveToolbox. New features are in bold.
Evaluation
The evaluation was carried out using a study derived from a listener study on drum loop similarity3. That study used a set of drum loop templates from FXpansion’s BFD3, whose raw (unquantised) information allows the use of microtiming features. It collected similarity scores from 21 participants on 80 pairs of drum loops.
After the correlation study, the authors found that drum loop similarity models built upon similarity metrics (baseline) performed best when combined with rhythm and microtiming features. Also, the new structural similarity metric alone (r=0.65, p=6.1e-11) performs better than the standard Hamming distance (r=0.59, p=9.7e-9). The fuzzy hamming distance, on the other hand, did not perform better than the standard one (r=0.56, p=6.1e-8).
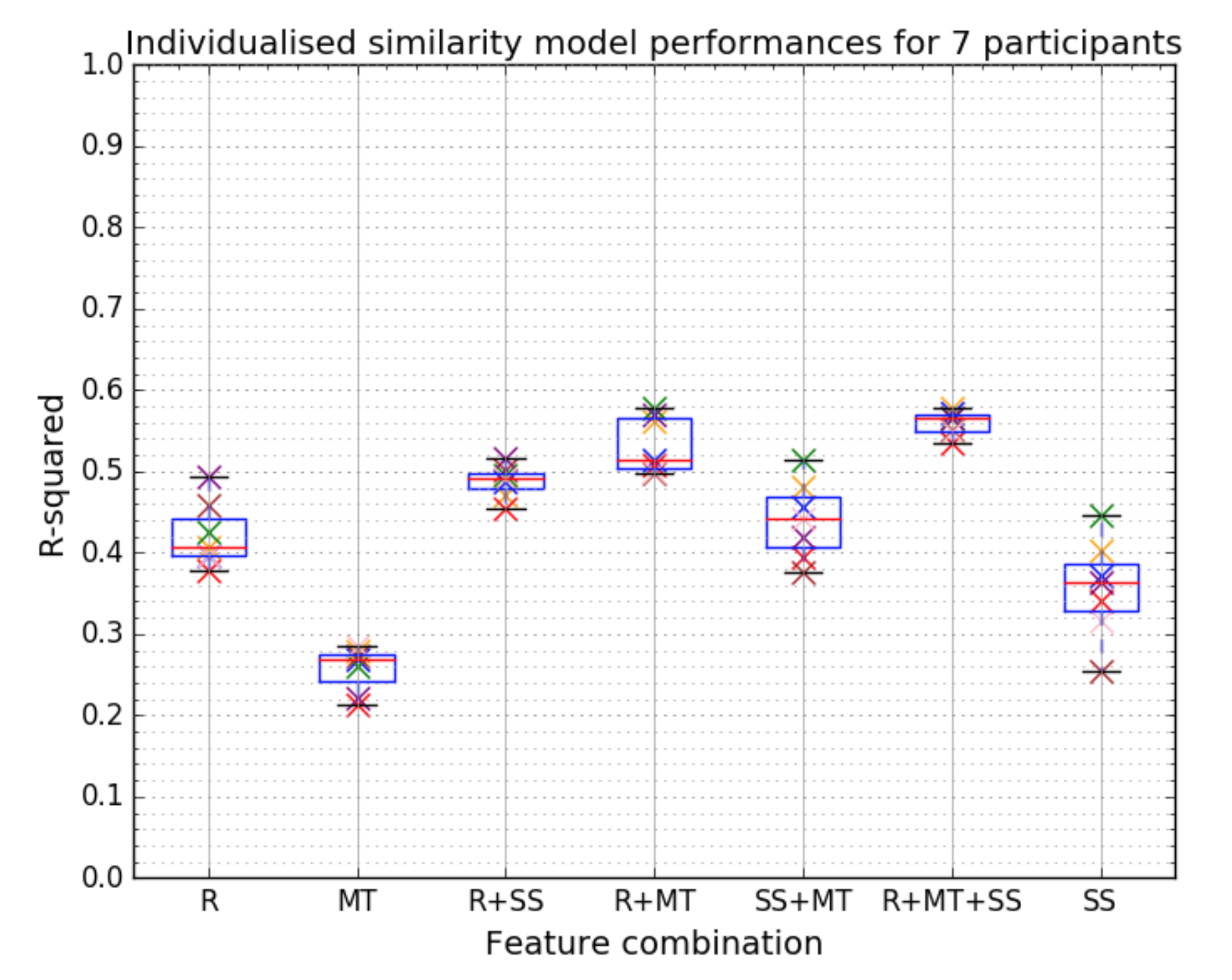
Model performance as R-squared value for rhythm R feature set, microtiming MT feature set, structural similarity feature SS and all three combined for each participant. The best performance is found when the three are combined.
Relevance
Extracting features from drum loops is an important yet relatively underexplored topic in MIR. Today, practically all commercial drum libraries include loop templates ready for the user to use and edit. There also exist datasets with a large number of these templates like the Groove MIDI Dataset4, ready to be imported to virtual instruments.
The features in this toolbox provide a quick and easy way to query drum loops that are perceptually similar to a target loop without one needing to explore the dataset manually. And, of course, this target loop could also be an automatic transcription of a drum performance or even a vocal imitation (beatboxing) performance. Such systems would allow music producers to quickly explore alternative drum loops for their compositions in an efficient and reliable way.
References
-
Bruford, F., Lartillot, O., McDonald, S., & Sandler, M. “Multidimensional similarity modelling of complex drum loops using the GrooveToolbox”, In Proceedings of the 21st Conference of the International Society for Music Information Retrieval (ISMIR), 2020. ↩
-
Sioros, G., Davies, M. E., & Guedes, C. “A generative model for the characterization of musical rhythms.”, Journal of New Music Research, 2018 ↩
-
Bruford, F., Barthet, M., McDonald, S., & Sandler, M. “Modelling Musical Similarity for Drum Patterns: A Perceptual Evaluation.” In Proceedings of the 14th International Audio Mostly Conference: A Journey in Sound, 2019. ↩
-
Gillick, J., Roberts, A., Engel, J., Eck, D., & Bamman, D. “Learning to groove with inverse sequence transformations.”, arXiv preprint arXiv:1905.06118, 2019. ↩